9 Sınıf Üslü Denklemler Konu Anlatımı

Tabanları eşit ve -1, 0, 1'den farklı iki 9 sınıf Üslü Denklemler konu anlatımı üslü ifade birbirine eşitse üsler birbirine eşittir.

Nesine Üyelik Iptal Formu

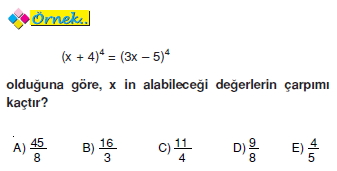
( (4x + 5y - 8)^{22} 2x - 3y + 7)^{44} = 0 ). ( dfrac{a}{m} = dfrac{b}{n} ). ( 9 sınıf Üslü Denklemler konu anlatımı quad x + 3 ne 0 Longrightarrow x ne -3 ).

Negatif kuvvette taban ters çevrilir. X, y (neq) 0 için x−n = (frac{1}{x^n}) ve ((frac{x}{y})^{-n} ((frac{y}{x})^n) olur. ( dfrac{25}{100} = 9 sınıf Üslü Denklemler konu anlatımı dfrac{1}{4} = 2^{-2} ).

Dinde Şans Var Mıdır

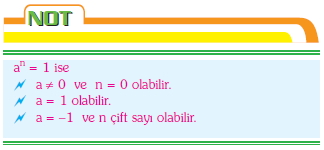
( dfrac{7x - y}{3} = -4 ). ( 2^6 + 7 9 sınıf Üslü Denklemler konu anlatımı cdot 7^y = 407 ). İfadeyi düzenleyelim. ( 16^{2(x - y)} = 16^2 ).

( dfrac{x}{2} = 9 sınıf Üslü Denklemler konu anlatımı dfrac{6}{4y} ). ( x^2 - 4x - 21 = 0 ). Üsler, en düşük olan üsse göre eşitlenebilir. 314 = 32. ( a^{16} = 16 ) ise ( a^{12} ) ifadesinin değeri kaçtır?.

Para Yatırmadan Bonus Veren Bahis Siteleri 2021

( 11^3 9 sınıf Üslü Denklemler konu anlatımı = 11^3 ). ( (y + 1)^2 x + y) - 1)^2 = 0 ).

Eşitliklerdeki tabanları 9 sınıf Üslü Denklemler konu anlatımı asal çarpanları cinsinden yazalım.

( x = 4 ) 9 sınıf Üslü Denklemler konu anlatımı ve ( y = -5 ). ( 4x + 5(2) - 8 = 0 ).

Almanya Sırbistan Maçı Izle

9 sınıf Üslü Denklemler konu anlatımı Üslü İfadeler 3. Bölüm Teknofem Video. ÖRNEK:. 3x = 34 olduğu için x = 4. Tüm terimleri eşitliğin sol tarafında toplayarak ifadeyi çarpanlarına ayıralım. ( x = dfrac{3}{5} ) bulunur. Tüm gerçek sayıların birinci kuvveti kendisidir. X1 = x olur.

9 sınıf Üslü Denklemler konu anlatımı ► 612 : 617 = 612−17 = 6−5. ► (−5)1 = −5. ( x^m = y^n ) ise,. ( x cdot y = dfrac{35}{24} ) bulunur. (x+1)12 = 212. ( 7^x = 64, quad 16^y = 49 ).

► ((frac{1}{2}))1 = (frac{1}{2}). Üsleri aynı olan üslü sayıların bölümünde tabanlar bölünür. Y (neq) 0 için xn : yn (frac{x}{y}))n olur.

Üslü Ifadeler Ve Denklemler 9. Sınıf

( (0,25)^{a + 4} = 32^{a + 4} ). ( 4^0 = 6^0 = 1 ). ÖRNEK:. 9 sınıf Üslü Denklemler konu anlatımı Her iki değer için de üs çift olduğu için bu iki değer geçerli birer çözümdür. İçinde üslü ifade bulunduran denklemlere üslü denklem adı verilir.

Betkolik Canlı Maç Izle

( (x + 5)^3 2x 9 sınıf Üslü Denklemler konu anlatımı - 1)^3 ) eşitliğini sağlayan ( x ) değerlerini bulun. ( -4x + 6y - 14 = 0 ). Bu değeri denklemlerden birinde yerine koyarak ( x ) değerini bulalım.

( t = 5^x = 5 Longrightarrow x = 1 ). ( 64^x = 243 Longrightarrow 2^{6x} = 3^5 ). 9 sınıf Üslü Denklemler konu anlatımı